ATOMS
Atom :
Atom, as a whole, is electrically neutral and therefore contains equal amount of positive and negative charges.
Thomson’s model:
In Thomson’s model, an atom is a spherical cloud of positive charges with electrons embedded in it.
Rutherford’s model:
In Rutherford’s model, most of the mass of the atom and all its positive charge are concentrated in a tiny nucleus (typically one by ten thousand the size of an atom), and the electrons revolve around it.
Rutherford nuclear model has two main difficulties in explaining the structure of atom:
(a) It predicts that atoms are unstable because the accelerated electrons revolving around the nucleus must spiral into the nucleus. This contradicts the stability of matter.
(b) It cannot explain the characteristic line spectra of atoms of different elements.
(a) It predicts that atoms are unstable because the accelerated electrons revolving around the nucleus must spiral into the nucleus. This contradicts the stability of matter.
(b) It cannot explain the characteristic line spectra of atoms of different elements.
Atoms of each element are stable and emit characteristic spectrum. The spectrum consists of a set of isolated parallel lines termed as line spectrum. It provides useful information about the atomic structure.
The atomic hydrogen emits a line spectrum consisting of various series. The frequency of any line in a series can be expressed as a difference of two terms;
Lyman series:
Balmer series:
Paschen series:
Brackett series:
Pfund series:
Lyman series:
Balmer series:
Paschen series:
Brackett series:
Pfund series:
To explain the line spectra emitted by atoms, as well as the stability of atoms, Neil’s Bohr proposed a model for hydrogenic (single electron) atoms. He introduced three postulates and laid the foundations of quantum mechanics:
(a) In a hydrogen atom, an electron revolves in certain stable orbits (called stationary orbits) without the emission of radiant energy.
(b) The stationary orbits are those for which the angular momentum is some integral multiple of h/2π. (Bohr’s quantization condition.) That is L = nh/2π, where n is an integer called a quantum number.
(c) The third postulate states that an electron might make a transition from one of its specified non-radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency (ν) of the emitted photon is then given by hν = Ei – Ef An atom absorbs radiation of the same frequency the atom emits, in which case the electron is transferred to an orbit with a higher value of n. Ei + hν = Ef
(a) In a hydrogen atom, an electron revolves in certain stable orbits (called stationary orbits) without the emission of radiant energy.
(b) The stationary orbits are those for which the angular momentum is some integral multiple of h/2π. (Bohr’s quantization condition.) That is L = nh/2π, where n is an integer called a quantum number.
(c) The third postulate states that an electron might make a transition from one of its specified non-radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency (ν) of the emitted photon is then given by hν = Ei – Ef An atom absorbs radiation of the same frequency the atom emits, in which case the electron is transferred to an orbit with a higher value of n. Ei + hν = Ef
As a result of the quantization condition of angular momentum, the electron orbits the nucleus at only specific radii. For a hydrogen atom it is given by,

The total energy is also quantized:
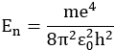
The n = 1 state is called ground state.
In hydrogen atom the ground state energy is –13.6 eV.
Higher values of n correspond to excited states (n > 1).
Atoms are excited to these higher states by collisions with other atoms or electrons or by absorption of a photon of right frequency.

The total energy is also quantized:
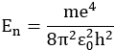
The n = 1 state is called ground state.
In hydrogen atom the ground state energy is –13.6 eV.
Higher values of n correspond to excited states (n > 1).
Atoms are excited to these higher states by collisions with other atoms or electrons or by absorption of a photon of right frequency.
De Broglie’s hypothesis that electrons have a wavelength, λ = h/mv gave an explanation for Bohr’s quantized orbits by bringing in the wave particle duality. The orbits correspond to circular standing waves in which the circumference of the orbit equals a whole number of wavelengths.
Bohr’s model is applicable only to hydrogenic (single electron) atoms. It cannot be extended to even two electron atoms such as helium. This model is also unable to explain for the relative intensities of the frequencies emitted even by hydrogenic atoms.
| Introduction to Atoms: | JJ Thompson atomic model |
| Alpha particle scattering: | Geiger-Marsden experiment |
| Rutherford’s model of an atom | |
| Total energy of electron in hydrogen atom | |
| Atomic spectra: | Spectral series of hydrogen |
| Empirical formulae for (wave number) of different series | |
| Bohr model of hydrogen atom: | Bohr’s postulates |
| Bohr radius | |
| Energy of electron in stationary states of hydrogen atom | |
| Line spectra of hydrogen atom: | Frequency of emitted radiation |
| Expression for Rydberg constant | |
| Energy level diagram | |
| De-Broglie’s explanation of Bohr’s second postulate | |
| Limitations of Bohr model | |
| Numerical Problems |
